알고리즘 준비하기 - 플로이드 워셜

🎯 플로이드-워셜 알고리즘

모든 최단 경로를 구하는 알고리즘이다.

이후에 정리할 다익스트라 알고리즘은 하나의 정점에서 다른 모든 정점까지의 최단 거리를 구하는 알고리즘이었다면, 플로이드-워셜 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있다.

💎 플로이드-워셜 알고리즘의 과정

모든 노드 간의 최단거리를 구해야 하는 것이 플로이드-워셜 알고리즘의 목표이다. 따라서 2차원 인접 행렬로 구한다. 알고리즘은 여러 라운드로 구성이 되는데 라운드마다 각 경로에서 중간 노드로 사용할 수 있는 노드를 선택하고, 더 짧은 길이를 선택하여 줄이는 과정을 반복한다.

[STEP 0] 그래프의 노드와 간선에 따라 최단 거리 테이블을 갱신한다.

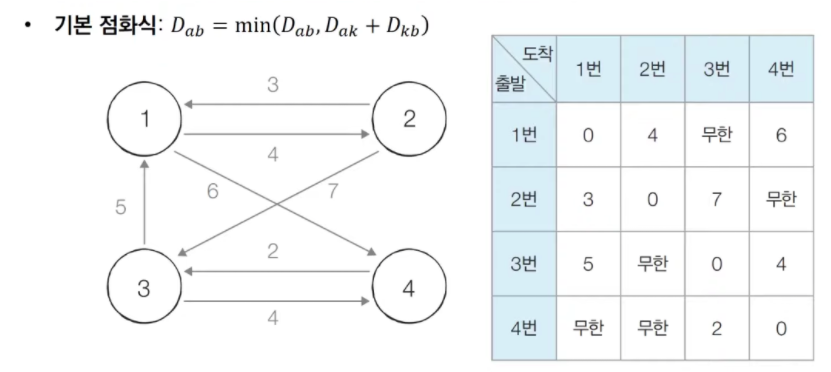
[STEP 1] 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

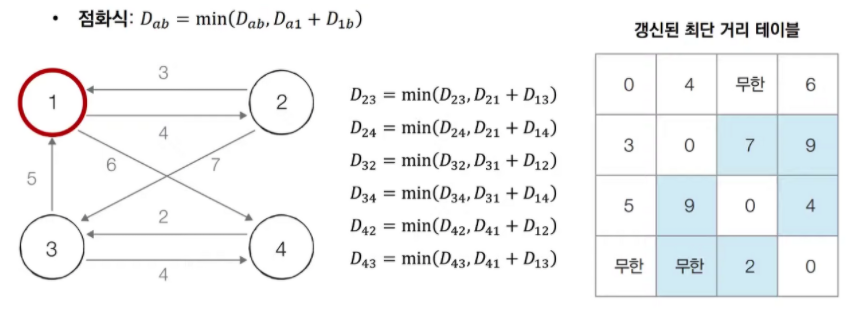
[STEP 2] 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

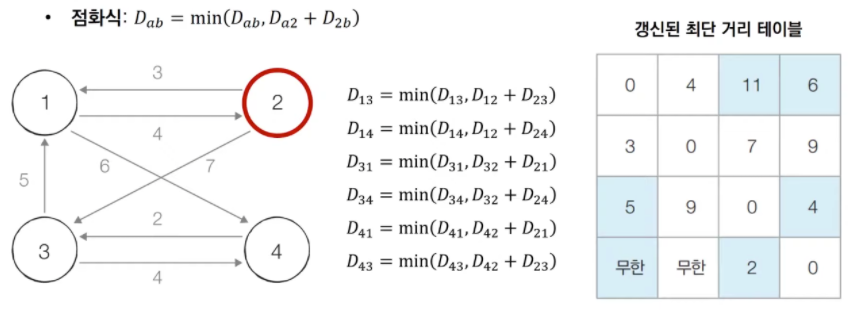
[STEP 3] 3번, 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

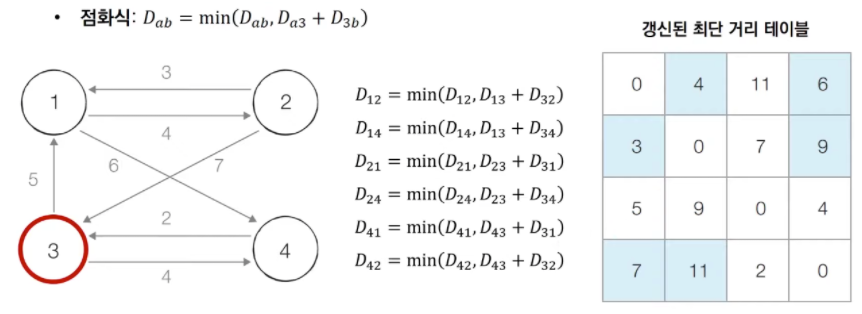
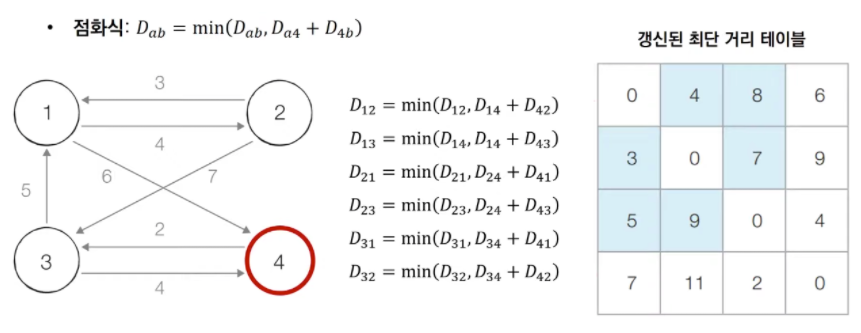
🎯 플로이드-워셜 알고리즘 코드 구현 (JS)

for(int k = 1; k<= n; k++){
    for(int i = 1; i <= n; i++){
        for(int j = 1; j<=n; j++){
            dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]);
        }
    }
}

플로이드-워셜 알고리즘은 3중 for문을 사용하기 때문에 시간 복잡도가 O(n^3)으로, 그래프의 크기가 작아 세제곱 시간 알고리즘을 적용해도 풀릴 때만 사용할 수 있다.

각 라운드별로 중간 노드가 될 노드 번호를 for문 가장 바깥의 k로 잡는다. 내부 이중 for문에는 i,j를 통해 각 노드별 모든 거리를 살펴보면서 k를 중간 노드로 삼을 때와 아닐 때의 값을 비교해 더 작은 값으로 업데이트 한다.