📚
알고리즘 준비하기 - 우선순위 큐
December 21, 2023
🎯 우선순위 큐
우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조의 일부이며 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
🎯 우선순위 큐의 구현 방법
크게 2가지로 분류할 수 있다. 배열로 구현하는 방법과 힙으로 구현하는 방법. 우선 배열로 구현하는 것은 구현 자체가 간단하다는 장점이 있지만 데이터를 삭제하거나 삽입해야하는 경우 모든 인덱스를 탐색해야 하는 과정이 있기 때문에 시간복잡도가 **O(N)**이 되므로 상대적으로 부족한 성능을 보여준다.
하지만 힙으로 구현하는 것은 구현 자체에서 난이도가 높지만 시간복잡도가 **O(logN)**이기 때문에 좋은 성능을 보여준다.
🎯 힙의 특징
그렇다면 힙의 특징은 무엇일까?
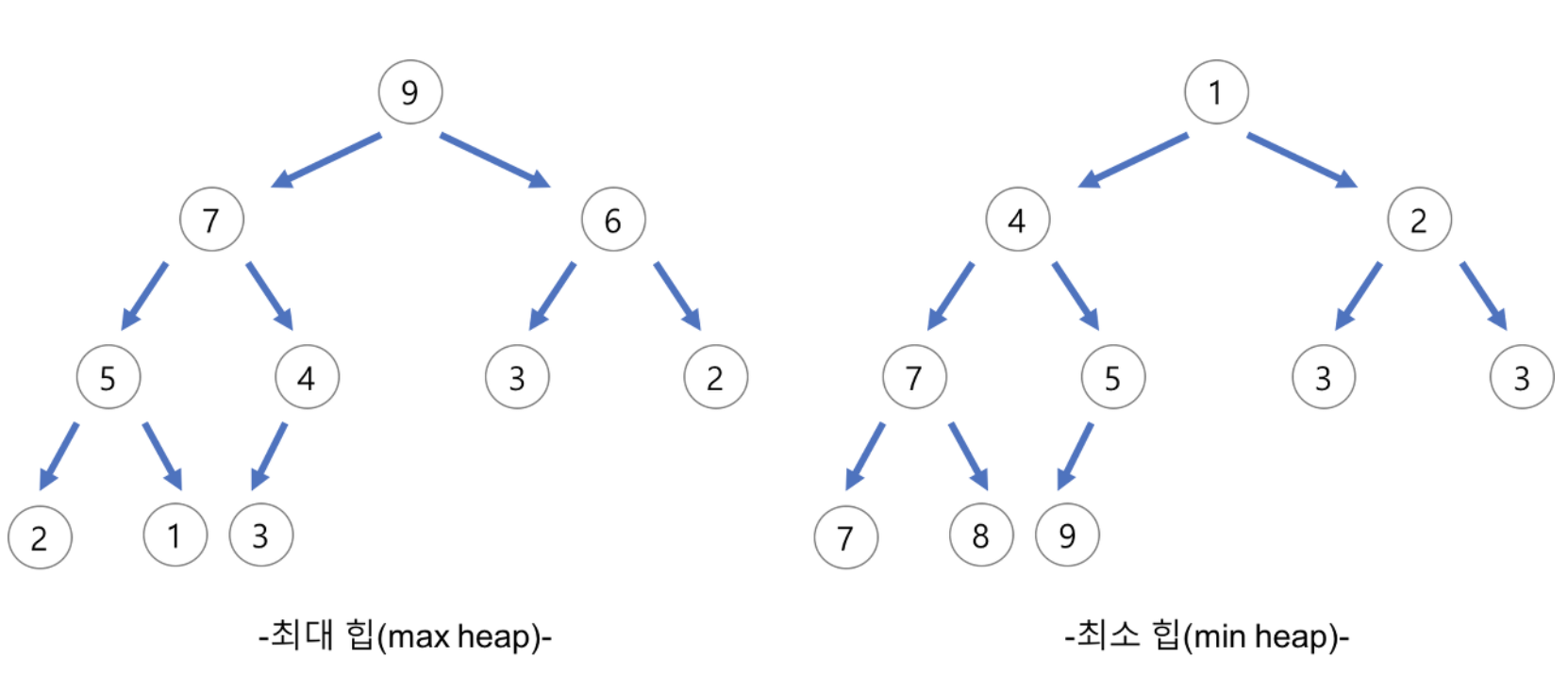
- 힙은 완전 이진 트리 자료구조이다.
완전 이진 트리란 마지막 레벨을 제외하고 모든 레벨이 모두 채워져있으며, 마지막 레벨의 모든 노드는 가능한 왼쪽에 위치한다. 즉, 루트 노드로부터 시작하여 왼쪽에서 오른쪽 자식 노드 순서대로 데이터가 순차적으로 삽입되는 트리를 의미한다.
- 최소 힙
루트 노드가 가장 작은 값을 가지며 값이 작은 데이터가 우선적으로 제거된다. 최소 힙은 부모 노드가 항상 자식 노드보다 값이 작다.
- 최대 힙
루트 노드가 가장 큰 값을 가지며 값이 큰 데이터가 우선적으로 제거된다. 최대 힙은 부모 노드가 항상 자식 노드보다 값이 크다.
- 힙의 인덱스 관계
좌측 자식 노드의 인덱스: 부모 노드의 인덱스 _ 2 우측 자식 노드의 인덱스: 부모 노드의 인덱스 _ 2 + 1 부모 노드의 인덱스: Math.floor(자식 노드의 인덱스 / 2)
최대 힙의 코드 구현 (JS)
class MaxHeap {
constructor() {
this.heap = [null]; // 이해하기 쉽게 0번째 Index는 null
}
heapPush(value) {
this.heap.push(value);
let currentIndex = this.heap.length - 1;
let parentIndex = Math.floor(currentIndex / 2);
while(parentIndex !== 0 && this.heap[parentIndex] < value) {
const temp = this.heap[parentIndex];
this.heap[parentIndex] = this.heap[currentIndex];
this.heap[currentIndex] = temp;
currentIndex = parentIndex;
parentIndex = Math.floor(currentIndex / 2);
}
}
heapPop() {
// 루트 노드밖에 없는 경우
if(this.heap.length === 2) return this.heap.pop();
let returnValue = this.heap[1];
this.heap[1] = this.heap.pop();
let currentIndex = 1;
let leftIndex = 2;
let rightIndex = 3;
while(this.heap[currentIndex] < this.heap[leftIndex] ||
this.heap[currentIndex] < this.heap[rightIndex]
) {
const temp = this.heap[currentIndex];
if (this.heap[leftIndex] < this.heap[rightIndex]) {
this.heap[currentIndex] = this.heap[rightIndex];
this.heap[rightIndex] = temp;
currentIndex = rightIndex;
} else {
this.heap[currentIndex] = this.heap[leftIndex];
this.heap[leftIndex] = temp;
currentIndex = leftIndex;
}
leftIndex = currentIndex * 2;
rightIndex = leftIndex + 1;
}
return returnValue;
}
heapReturn() {
return this.heap;
}