알고리즘 연습하기 - BFS의 3차원적 접근
우선 BFS 알고리즘의 기본 개념은 알고리즘 준비하기 -BFS 에 잘 정리해두었으니 참고하면 좋을 것 같다.
👉 문제 확인하기 : BOJ - 벽 부수고 이동하기
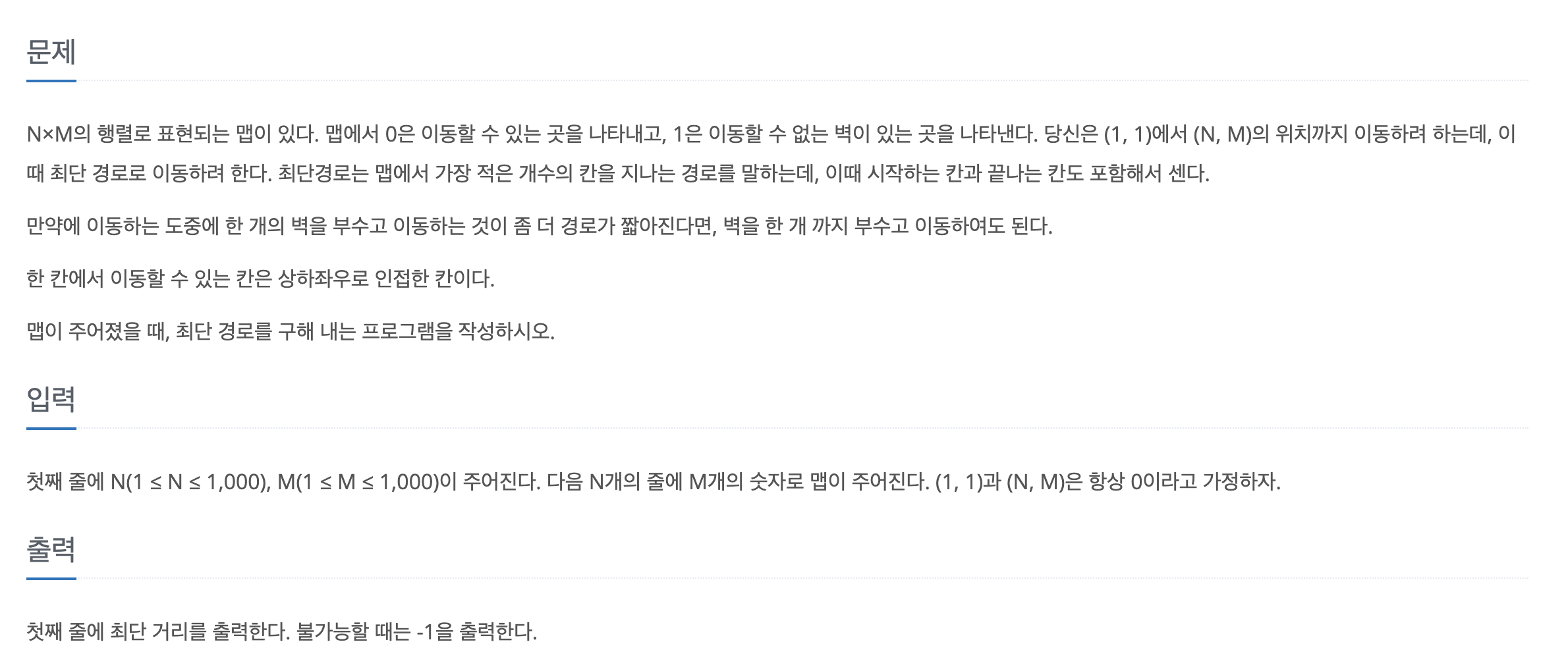
🎯 문제
🎯 접근 방법
우선 이번 포스트를 작성하게 된 계기는 문제를 풀면서 끝없는 메모리 초과 문제때문이었다. 다른 사람들의 풀이를 보면 3차원 배열을 사용하여 접근하였지만 2차원 배열만으로도 충분히 문제가 풀렸기에 내 풀이에 고집이 있었다.
💎 1차 시도 (❌)
다른 사람들의 게시판 글 후기를 보면 큐(Queue)를 구현하는 것에 있어서 시간초과가 많이 발생했다고 한다. 다양한 BFS 문제를 겪어본 결과 Node.js에서는 무조건 Queue를 직접 구현해서 사용해야 한다. 즉 shift를 사용하는 순간 어마무시한 배열을 한칸식 옮겨줘야 하기 때문에 사용을 지양한다.
여기까지는 별 문제가 없었다.
벽을 1번은 깰 수 있다고 하는데 그렇다면 백트래킹을 이용해서 배열에 있는 모든 1을 0으로 한번씩 바꿔서 BFS를 돌리면 되지 않을까..? 했다. 모든 예외 케이스는 통과가 됐지만 메모리 초과 문제가 해결되지 않았다. 실제로 나와 같이 생각한 사람이 있었기에 아래 링크에서 해당 문제를 해결할 수 있었다.
한마디로 정리하자면 벽이 최대 O(NM)개 있는 맵에서, 벽을 하나 부술 때마다 O(NM)개의 칸을 탐색해야 하기 때문에 시간복잡도가 O((NM)^2)이 된다. 이 수는 우리가 대충 1초에 돌 수 있다고 보는 단위인 1억을 10000배나 뛰어넘는 1조이기 때문에 절대 통과될 수 없다.
💎 2차 시도 (⭕️)
사실 이 문제는 3차원 배열을 이용하지 않고서는 해결할 수 없는 문제였다. 이해하는데 정말 오래걸리기는 했지만 다른 BFS 심화문제를 해결하는 것에 있어서 큰 도움이 될 것 같다.
결국 방문체크(방문배열)란 것은, BFS에서 ‘모든 경우’를 살펴보며 진행할 때, 같은 행위를 두번하면 비효율적이니 그걸 막기 위해 사용한다. 따라서 방문배열은 BFS를 진행할 때 탐색할 수 있는 ‘모든 경우’를 나타낼 수 있어야 한다. 일반적인 BFS 탐색 문제에서 모든 경우는 결국 ‘이 위치에 이미 왔었다’면 된다.
그럼 좀 더 확장해서 생각해보자. 위 미로 문제에서 장애물(‘X’ 부분)을 한 번까지는 부수고 이동할 수 있다고 하자. 그럼 ‘모든 경우’가 변한다. 말로 하자면 ‘해당 위치에 장애물을 부순 상태로 이미 왔었거나, 해당 위치에 아직 장애물을 부수지 않은 상태로 이미 왔었다.‘가 된다. 이걸 표현하려면 방문배열이 다음과 같이 변경되야 한다. 여기서 1차와 2차는 동일하고, 3차는 0일 경우 아직 장애물을 부수지 않은 경우, 1일 경우 장애물을 부순 경우에 대해 체크하면 된다. 예를들어 visited[0][0][0]은 처음 시작하는 S의 위치이다. 이후 아래로 장애물을 부수며 한 번 내려갔다. 원래대로면 다시 S 지점으로 못돌아와야하지만 여기서는 장애물을 부쉈는지도 체크하기 때문에 되돌아올 수 있으며 visited[0][0][1]이 체크 되게 된다.
한마디로 visited[X][y][isBreak]는 (X,Y)라는 좌표에 도착했을 때 isBreak가 0이라면 벽을 부수지 않은 상태의 거리 값을, isBreak가 1이라면 한번 벽을 부순 상태에서 계산된 거리 값을 가지고 있는 상태인 것이다.
자세한 구현은 아래 주석과 함께 정리된 코드를 살펴보면 된다.
🎯 해결 코드 (JS)
let fs = require('fs');
let input = fs.readFileSync('example.txt').toString().split('\n');
const [N, M] = input.shift().split(' ').map(Number);
let board = [];
let result = [];
input.forEach((value) => board.push(value.split('').map(Number)));
let visited = Array.from({ length: N }, () => Array.from({ length: M }, () => Array(2).fill(0)));
class Queue {
constructor() {
this.store = {};
this.front = 0;
this.rear = 0;
}
size() {
if (this.store[this.rear] === undefined) return 0;
else return this.rear - this.front + 1;
}
push(value) {
if (this.size() === 0) this.store['0'] = value;
else {
this.rear += 1;
this.store[this.rear] = value;
}
}
popLeft() {
let temp;
if (this.front === this.rear) {
temp = this.store[this.front];
delete this.store[this.front];
this.front = 0;
this.rear = 0;
return temp;
} else {
temp = this.store[this.front];
delete this.store[this.front];
this.front += 1;
return temp;
}
}
}
function BFS() {
let queue = new Queue();
queue.push([0, 0, 0]);
visited[0][0][0] = 1;
while (queue.size()) {
const [X, Y, isBreak] = queue.popLeft();
if (X === N - 1 && Y === M - 1) return visited[X][Y][isBreak];
const dX = [-1, 1, 0, 0];
const dY = [0, 0, -1, 1];
for (let i = 0; i < 4; i += 1) {
const [aX, aY] = [X + dX[i], Y + dY[i]];
if (aX >= 0 && aX < N && aY >= 0 && aY < M) {
// 다음이 벽이 아니고 방문한 적이 없는 경우
if (board[aX][aY] === 0 && visited[aX][aY][isBreak] === 0) {
visited[aX][aY][isBreak] = visited[X][Y][isBreak] + 1;
queue.push([aX, aY, isBreak]);
}
// 다음이 벽이고 방문한 적이 없는 경우
else if (board[aX][aY] === 1 && visited[aX][aY][isBreak] === 0) {
if (isBreak === 0) {
visited[aX][aY][1] = visited[X][Y][isBreak] + 1;
queue.push([aX, aY, 1]);
} else if (isBreak === 1) continue;
}
}
}
}
return -1;
}
console.log(BFS());