🎯 LIS(최장 증가 부분 수열)

원소의 개수가 N개인 배열이 있다고 가정을 해보자. 배열의 원소 index는 변하지 않는 조건 하에 각 원소가 이전 원소보다 큰, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다.

🎯 이분탐색을 활용한 LIS

LIS 알고리즘을 구현하는 방법은 여러가지가 있지만 이분탐색을 이용한 방법은 효율적으로 구현할 수 있다. 일반적으로 이분탐색은 O(logN)에 탐색이 가능하기 때문에 LIS를 구현하는 문제에서는 O(NlogN)의 시간복잡도로 문제를 해결할 수 있다.

위 이분탐색을 이용하여 LIS를 구하는 코드는 아래와 같다.

let inputNumber = input.shift().split(' ').map(Number);
let LIS = [];

// LIS 배열에서 인덱스 값보다 작은 값이 나왔을 경우에 실행될 함수
function BinarySearch(left, right, target) {
  let mid;

  while (left < right) {
    mid = Math.floor((left + right) / 2);

    if (LIS[mid] < target) left = mid + 1;
    else right = mid;
  }

  return right;
}

LIS[0] = inputNumber[0];
let j = 0; // LIS 비교 인덱스
let i = 1; // 원래 배열 비교 인덱스

while (i < N) {
  if (LIS[j] < inputNumber[i]) {
    LIS[j + 1] = inputNumber[i];
    j += 1;
  } else {
    let index = BinarySearch(0, j, inputNumber[i]);
    LIS[index] = inputNumber[i];
  }

  i += 1;
}

🎯 실제 LIS에 해당하는 배열 구하기

위 방법은 LIS의 길이를 구하는 방법이다. 따라서 실제 해당 길이에 포함되는 배열을 구하고 싶을 때는 추가적인 작업이 필요하다.

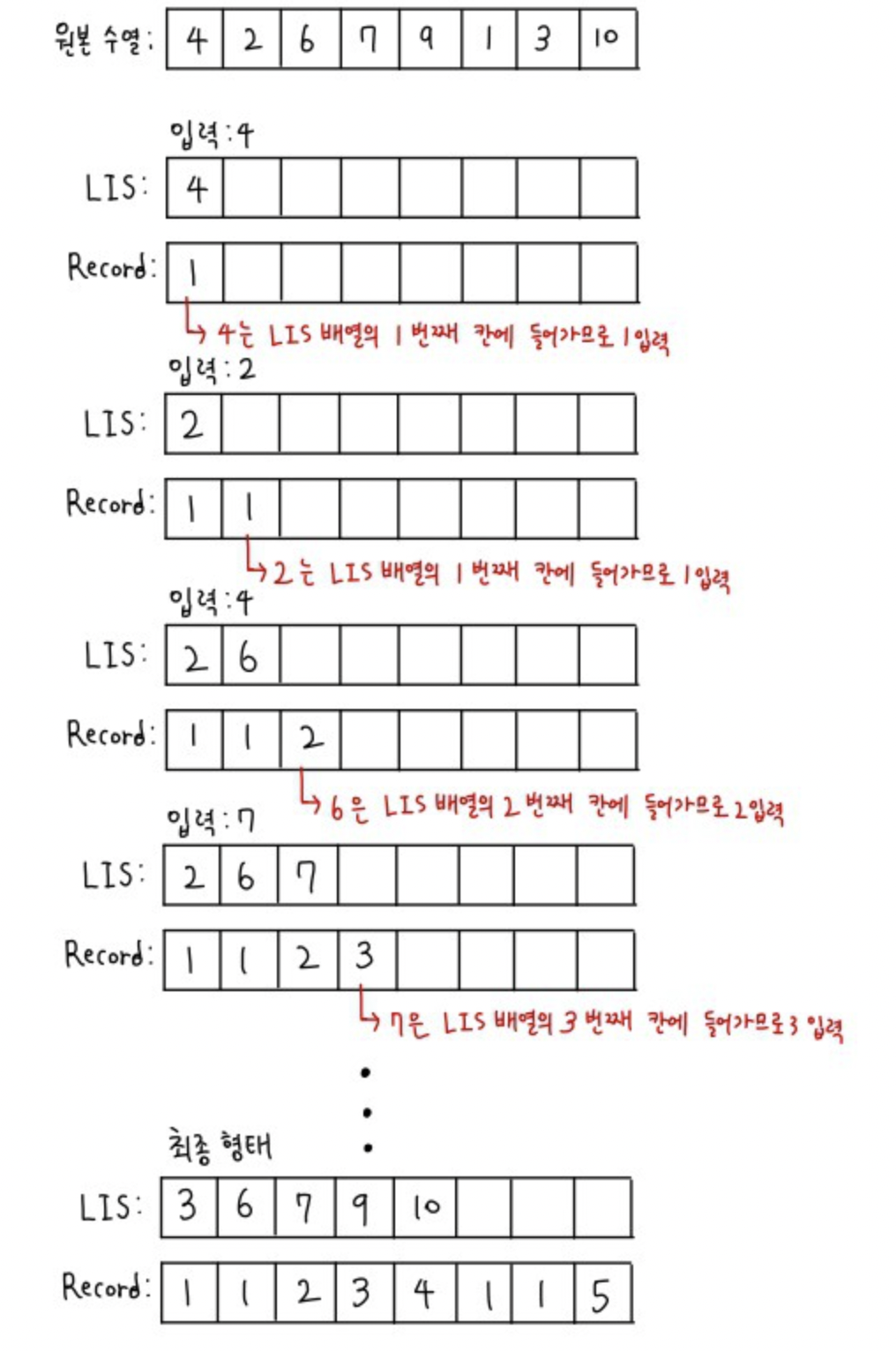
  1. 위에서 살펴봤던 LIS를 구하는 과정처럼 LIS 배열과 Record라는 배열을 생성한 후 LIS 배열에는 기존 과정을, Record라는 배열에는 LIS 몇번 째 배열에 값이 입력되는지 index 값을 순차적으로 적어준다.

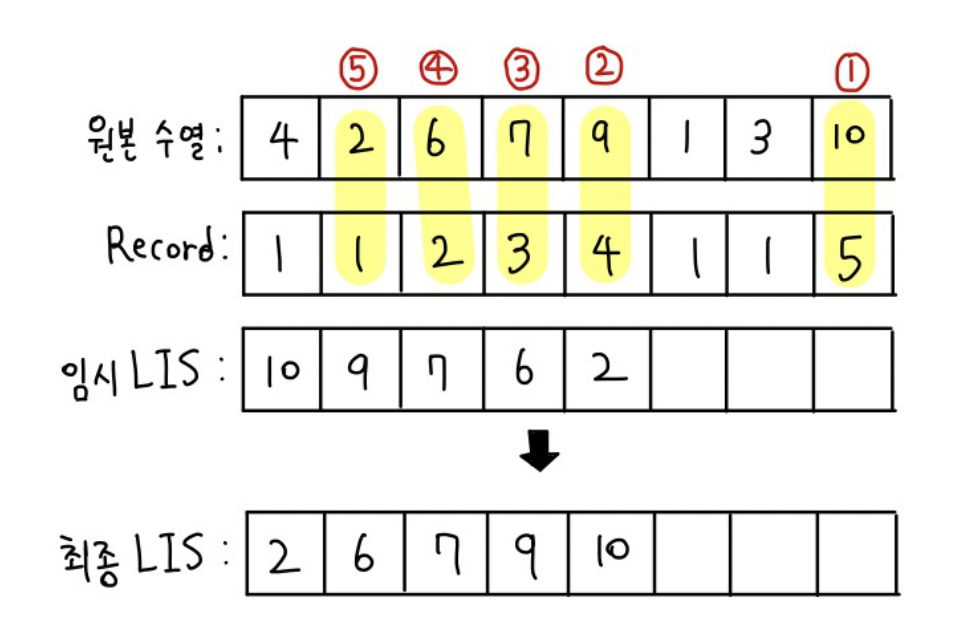
  2. 이후에 한번 순회하게 된다면 Record 배열의 최대값으로부터 거꾸로 순회하며 해당 인덱스에 해당하는 원본 수열의 값을 임시 LIS에 넣어주고 최대값을 1씩 줄여나간다.

  3. 임시 LIS를 오름차순으로 정렬한다.

  4. 해당 배열이 실제 LIS에 해당하는 결과값이다.

📑 Reference

그림 출처 : 방앗간 개발자