알고리즘 연습하기 - 피보나치 수열

🎯 분할 정복을 통한 피보나치 수열의 이해

문제를 확인해보면 n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다. 우리가 흔히 아는 F(N+2) = F(N+1) + F(N) 공식을 적용한다면 n이 너무 크기 때문에 시간초과가 발생한다.

저 공식 말고는 마땅히 생각나는 공식이 없었다. 구글의 도움을 받으려고 하니 행렬을 이용한다면 피보나치 수열 문제를 빠르게 해결할 수 있었다.

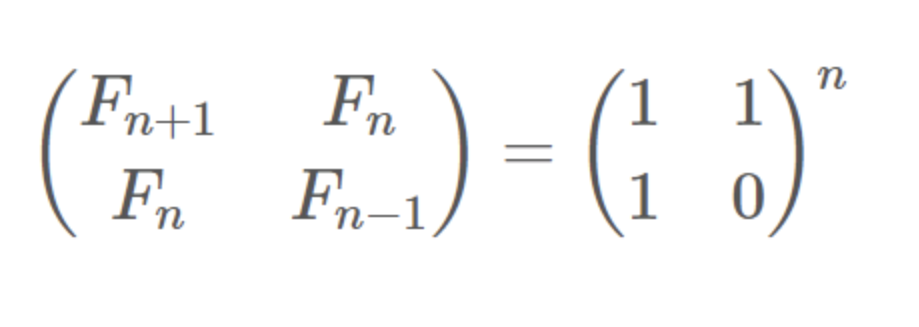
만약 2의 N제곱의 값이 2의 A제곱 + 2의 B제곱이라고 한다면 N = A+B로 나타낼 수 있다. 이와 같은 원리를 위 그림에 적용해보자.

[[F(N+1), F(N)], [F(N), F(N-1)]]과 같은 행렬은 [[F(A+1), F(A)], [F(A), F(A-1)]] + [[F(B+1), F(B)], [F(B), F(B-1)]]로 만들 수 있다.

그리고 이제부터 구하고자 하는 값이 홀수일 때와 짝수일 때로 나뉠 수 있는데

먼저 홀수일 때에는 위에서 보이는 F(N-1)을 행렬의 곱셈공식을 통해 나타내면 F(N-1) = F(A) x F(B) + F(A-1) x F(B-1)이다. 하지만 A와 B는 같다고 놓아도 상관없기 때문에 모든 것을 A로 통일시키면 F(2A-1) = F(A)^2 + F(A-1)^2으로 표현이 가능하다.

마찬가지로 짝수일 때를 적용하기 위해서는 F(N)을 행렬의 곱셈공식으로 표현할 필요가 있다. F(N) = F(A+1) x F(B) + F(A) x F(B-1)이다. 위와 같이 적용시키면 F(2A) = (2F(A+1) - F(A)) x F(A)로 표현이 가능하다.

위와 같이 점화식을 세워두면 작은 값을 통해서라도 큰 결과를 얻어낼 수 있다는 장점이 있다.

🎯 피보나치 수열의 핵심 점화식

N이 홀수일 때 N = 2A - 1 A = N+1 / 2 F(A)^2 + F(A-1)^2
N이 짝수일 때 N = 2A A = N / 2 (2 x F(A-1) + F(B)) * F(B)

🎯 코드 구현 (JS)

애초에 수가 어마무시하게 크기 때문에 반드시 BigInt를 사용해줘야만 한다. BigInt를 사용시에는 숫자 뒤에 n을 붙여줘야 오류가 발생하지 않는다. 또한 출력값은 String형태여야 n이 같이 출력되지 않는다.

const N = BigInt(input[0]);
let P = 1000000007n; // BigInt 리터럴은 끝에 'n'을 붙입니다.

// 피보나치 값 기본 세팅
let map = new Map();
map.set(0n, 0n); // BigInt 리터럴은 끝에 'n'을 붙입니다.
map.set(1n, 1n);
map.set(2n, 1n);
map.set(3n, 2n);

// 피보나치 계산 함수
function Fibonacci(index) {
  if (map.has(index)) return map.get(index);
  // 인덱스가 짝수인 경우
  else if (index % 2n === 0n) {
    let nIndex = index / 2n;
    let fibonacciA = Fibonacci(nIndex - 1n);
    let fibonacciB = Fibonacci(nIndex);
    let value = (2n * fibonacciA + fibonacciB) * fibonacciB;
    let result = value % P;

    map.set(index, result);
    return result;
  }

  // 인덱스가 홀수인 경우
  else if (index % 2n === 1n) {
    let nIndex = (index + 1n) / 2n;
    let fibonacciA = Fibonacci(nIndex);
    let fibonacciB = Fibonacci(nIndex - 1n);
    let value = fibonacciA ** 2n + fibonacciB ** 2n;
    let result = value % P;

    map.set(index, result);
    return result;
  }
}

console.log(Fibonacci(N).toString());

🎯 분할 정복을 통한 피보나치 수열의 이해
🎯 피보나치 수열의 핵심 점화식
🎯 코드 구현 (JS)