알고리즘 준비하기 - 에라토스테네스의 체
🎯 에라토스테네스의 체
백준, 프로그래머스 문제를 풀다보면 정말 많이 등장하는 유형이 바로 소수 찾기 이다. 에라토스테네스의 체 는 바로 소수를 찾는 방법 중 하나이다.
알고리즘의 원리는 다음과 같다.
-
숫자 2를 시작으로 2를 빈 곳에 적어두고, 정해진 숫자의 범위의 마지막 숫자까지 모든 2의 배수를 제거한다.
-
다음 숫자인 3을 빈 곳에 적어두고, 정해진 숫자의 범위의 마지막 숫자까지 모든 3의 배수를 제거한다.
-
4는 제거했기 때문에 다음 숫자인 5로 넘어간다. 정해진 숫자의 범위의 마지막 숫자까지 모든 5의 배수를 제거한다.
-
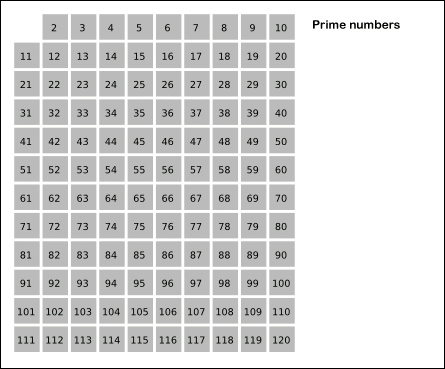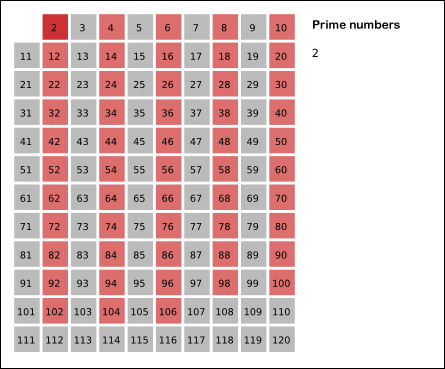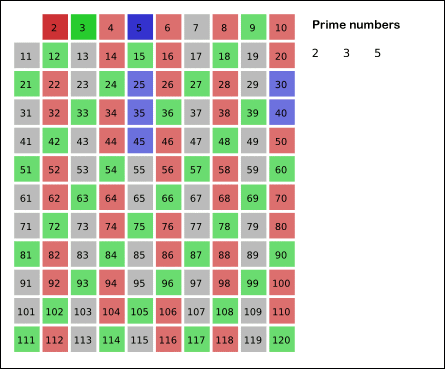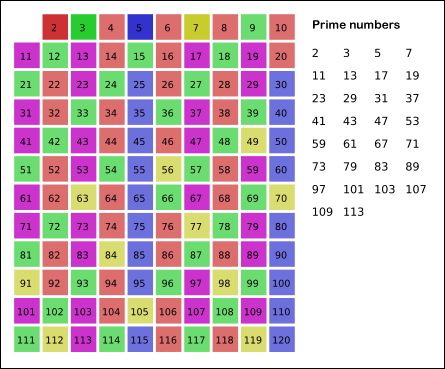
위 과정을 마지막 숫자까지 반복한다.
-
빈 곳에 적어둔 숫자가 소수에 해당한다.
🎯 메모리를 효율적으로 관리하는 방법
위에서 설명하는 과정을 조금 더 분석해보면 정해진 숫자의 범위의 마지막 숫자까지의 수의 제곱근까지만 반복문을 진행해 배수를 제거하면 된다.
예를 들어 120까지의 숫자를 순회하면서 소수를 찾는 과정이라면 11^2 > 120인 11까지만 배수를 제거하고, 그 이후의 모든 숫자들은 모두 소수이기 때문에 순회하지 않아도 된다.
처음에는 이해하지 못했던 부분이었지만 직접 계산하면서 깨달았다. 이렇게 진행된다면 메모리 공간을 조금 더 효율적으로 사용할 수 있을 것이다.
🎯 에라토스테네스의 체 코드 구현 (JS)
function isPrime(Num) {
let numberArr = Array(Num + 1)
.fill(true)
.fill(false, 0, 2);
for (let i = 2; i * i <= Num; i += 1) {
if (numberArr[i]) {
for (let j = i * 2; j <= Num; j += i) {
numberArr[j] = false;
}
} else continue;
}
}우선 정해진 숫자까지의 배열을 모두 true로 설정하고 인덱스가 0과 1인 부분만 false로 바꿔주는 기본적인 설정을 해준다. (소수는 2부터 적용이 되기 때문) 그리고 배열을 모두 순회하면서 배열의 값이 true라면 해당 값의 배수인 값을 모두 false로 바꿔주고, false라면 다음 수부터 다시 순회한다.
🎯 시간 복잡도
에라토스테네스의 체 시간 복잡도는 O(Nlog(log N))이다.
N이하의 소수를 판별하는 것만 따지면 O(NlongN)이다.
하지만 여기서 이미 배수로 체크된 수는 나누지 않고 넘어간다. 즉, 최종적으로 정리하면 총 시간복잡도는 O(Nlog(log N))임을 알 수 있다.
거의 선형 시간에 해결할 수 있을 정도로 빠른 시간에 해결이 가능하다.