알고리즘 준비하기 - 이진 트리와 이진 순회
🎯 트리
트리는 계층적인 자료를 표현하는 데 사용되는 자료구조이다.
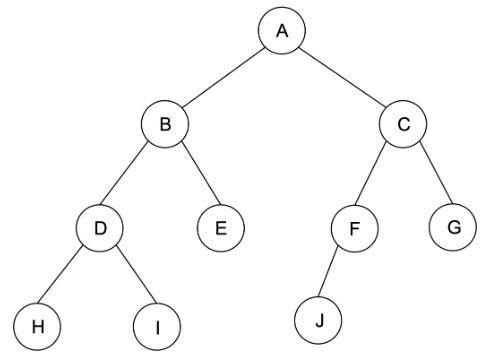
Node tree의 각 요소를 노드라고 한다. B를 A의 자식 노드, A를 B의 부모 노드라고 한다. 각 Node는 자신의 데이터를 가지고 있으며, 자식 노드의 주소를 가지고 있을 수도 있다.
Root Node A와 같이 부모 노드가 없고 최상단에 위치한 Node를 루트 노드라고 한다.
Leaf Node H, I, E, J, G처럼 자식 노드가 없는 노드를 Leaf Node라고 한다.
Size 모든 Node의 갯수를 크기라고 한다.
Depth Root Node로부터의 거리를 깊이라고 한다.
🎯 이진 트리
자식 노드의 갯수가 최대 2개로 한정된 tree를 말한다.
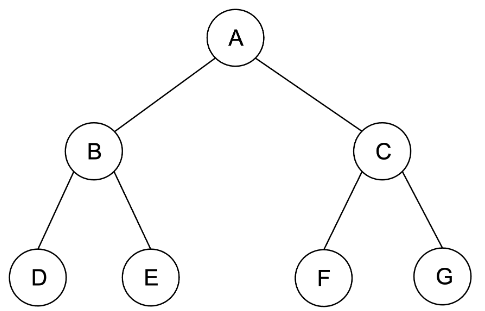
최대 자식 노드 갯수가 2개인 것 뿐이므로 위 그림에서 G노드가 없어도 이진 트리이다.
🎯 이진 탐색 트리
이진 탐색이 동작할 수 있도록 고안된 자료구조의 일종이다. 왼쪽 자식 노드가 부모 노드보다 작고 오른쪽 자식 노드가 부모 노드보다 큰 이진 트리를 말한다.
왼쪽 자식 < 부모 노드 < 오른쪽 자식
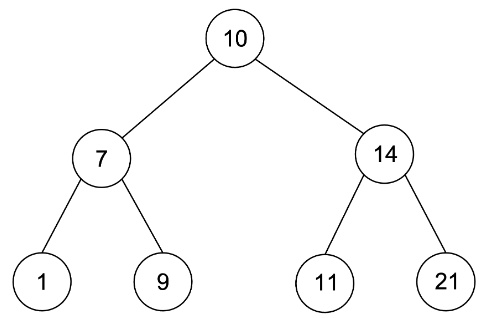
위와 같은 조건이 성립하면 원하는 값을 찾고싶을 때 해당 값을 Root Node값과 비교하여 왼쪽 혹은 오른쪽으로 탐색해 나갈 수 있다.
🎯 트리 순회
트리 자료구조에 포함된 노드를 특정한 방법으로 한번 씩 방문하는 방법을 의미한다. 보통 자신을 출력하는 방법과 같이 방문한 노드를 시각적으로 확인이 가능하다.
대표적으로 트리 순회 방법은 3가지가 있다.
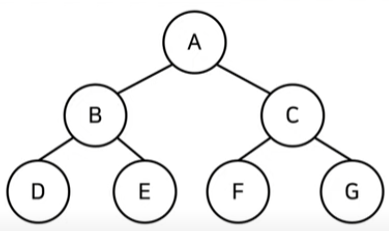
💎 In Order (중위 순회)
- 왼쪽 노드부터 출력한다.
- 이후 루트 노드를 출력한다.
- 이후 오른쪽 노드를 출력한다.
위의 트리를 중위 순회하면 D-B-E-A-F-C-G 이다.
💎 Pre Order (전위 순회)
- 루트 노드부터 출력한다.
- 이후 왼쪽 노드를 출력한다.
- 이후 오른쪽 노드를 출력한다.
위의 트리를 중위 순회하면 A-B-D-E-C-F-G 이다.
💎 Post Order (후위 순회)
- 왼쪽 노드부터 출력한다.
- 이후 오른쪽 노드를 출력한다.
- 이후 루트 노드를 출력한다.
위의 트리를 중위 순회하면 D-E-B-F-G-C-A 이다.
🎯 이진 트리 및 이진 순회 구현하기 (JS)
class BinarySearchTree {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
insert(value) {
if (value < this.value) {
if (this.left === null) this.left = new BinarySearchTree(value);
else this.left.insert(value);
} else if (value > this.value) {
if (this.right === null) this.right = new BinarySearchTree(value);
else this.right.insert(value);
}
}
preOrder(callback) {
callback(this.value);
if (this.left) this.left.preOrder(callback);
if (this.right) this.right.preOrder(callback);
}
inOrder(callback) {
if (this.left) this.left.inOrder(callback);
callback(this.value);
if (this.right) this.right.inOrder(callback);
}
postOrder(callback) {
if (this.left) this.left.postOrder(callback);
if (this.right) this.right.postOrder(callback);
callback(this.value);
}
}
const newNode = BinarySearchTree(input.shift());
let array = [];
newNode.postOrder((value) => array.push(value));🎯 예제 확인하기
👉 문제 확인하기 : BOJ - 트리 순회
const N = Number(input.shift());
let tree = {};
for (let i = 0; i < N; i += 1) {
const [node, left, right] = input[i].split(' ');
tree[node] = [left, right];
}
let result = '';
function inOrder(node) {
if (node !== '.') {
const [LC, RC] = tree[node];
inOrder(LC);
result += node;
inOrder(RC);
} else return;
}
function preOrder(node) {
if (node !== '.') {
const [LC, RC] = tree[node];
result += node;
preOrder(LC);
preOrder(RC);
} else return;
}
function postOrder(node) {
if (node !== '.') {
const [LC, RC] = tree[node];
postOrder(LC);
postOrder(RC);
result += node;
} else return;
}
preOrder('A');
result += '\n';
inOrder('A');
result += '\n';
postOrder('A');
console.log(result);