알고리즘 준비하기

🎯 벨만 포드

벨만 포드 알고리즘은 유향 그래프에서 최단 경로를 계산할 때 이용되는 알고리즘이다. 하지만 의문이 든다. 이전 포스트에서 유향 그래프 최단 경로를 계산할 때 다익스트라 알고리즘을 사용한다고 했었기 때문이다. 하지만 벨만 포드 알고리즘이 다익스트라 알고리즘과 가장 큰 차이를 보이는 곳은 가중치의 음수 여부 이다.

다익스트라 알고리즘은 벨만 포드 알고리즘과 동일한 작업을 수행하지만 실행속도는 더 빠르다.

그렇다면 똑같이 최단 경로를 구하는 알고리즘인데 왜 가중치가 음수일 때 벨만 포드 알고리즘을 사용해야 할까? 이 질문에 답으로 아래와 같은 그래프를 한번 살펴보자.

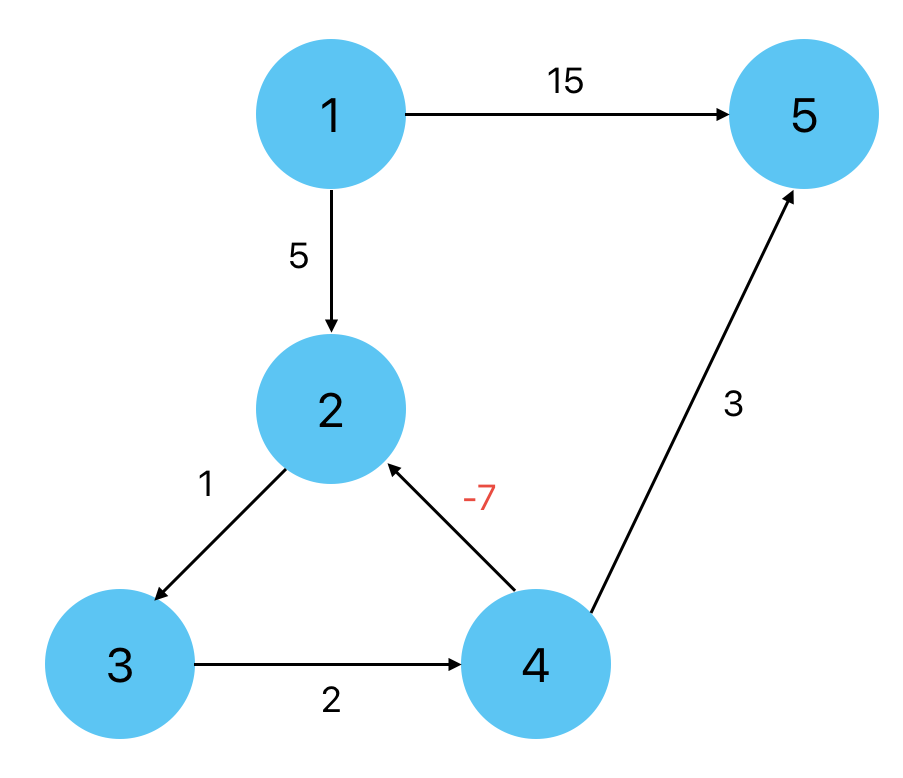
만약 위 그래프에서 시작 노드가 2인 경우를 생각해보자. 만약 4에서 2로 가는 가중치가 양수이고, 다익스트라 알고리즘을 사용했을 경우 2 - 3 - 4를 순회하고 절대 2로 다시 돌아가지 않는다. 왜냐하면 가중치 합의 최소값이 2 - 3 - 4 이후에는 갱신될 수 없기 때문에 큐에는 노드 4가 남는다.

하지만 4에서 2로 가는 가중치가 음수인 경우에는 합을 계산하면 계산할 수록 최소값이 되기 때문에 음의 무한대가 되는 현상이 발생한다. 따라서 이 때에는 벨만 포드 알고리즘을 사용하여 음의 사이클을 없애는 방향으로 진행되어야 한다.

🎯 음의 사이클 감지

간단하게 설명하지면 벨만 포드 알고리즘에서는 음의 사이클이 처음으로 감지된다면 최단 거리를 찾을 수 없는 반환값을 return하게 된다.

모든 노드까지의 거리를 Infinity로 초기화하고, 출발 노드의 거리는 0으로 초기화한다.
모든 간선을 탐색하여 최단 거리를 갱신한다.
2번의 과정을 노드의 개수 -1번 반복한다.
3번까지의 과정에서 이미 최단 거릭 갱신이 완료되어야 한다. 그렇기 때문에 만약 2번의 과정을 한번 더 수행했을 때 최단 거리가 갱신된다면 음의 사이클이 존재한다고 판단한다. 음의 사이클이 존재한다면 최단 거리를 구하는 것이 불가능함을 알려야 한다.

🎯 코드 구현 과정 (JS)

👉 관련 문제 풀어보기 : BOJ - 타임머신

// 시작점과 종점, 가중치가 담겨 있는 배열 생성
let paths = [];
for (let i = 0; i < M; i += 1) {
  paths.push(input[i].split(' ').map(Number));
}

// 거리의 값을 갱신할 수 있는 배열 생성
let distance = Array(N + 1).fill(Infinity);

function BellmanFord(start, n, path, dist) {
  dist[start] = 0;
  let update = false;

  for (let i = 1; i <= n; i += 1) {
    update = false;
    for (let j = 0; j < path.length; j += 1) {
      const [from, to, weight] = path[j];

      if (dist[from] + weight < dist[to]) {
        dist[to] = dist[from] + weight;
        update = true;
      }
    }
    if (!update) return false;
    if (update && i === n) return true;
  }
}

🎯 벨만 포드
🎯 음의 사이클 감지
🎯 코드 구현 과정 (JS)